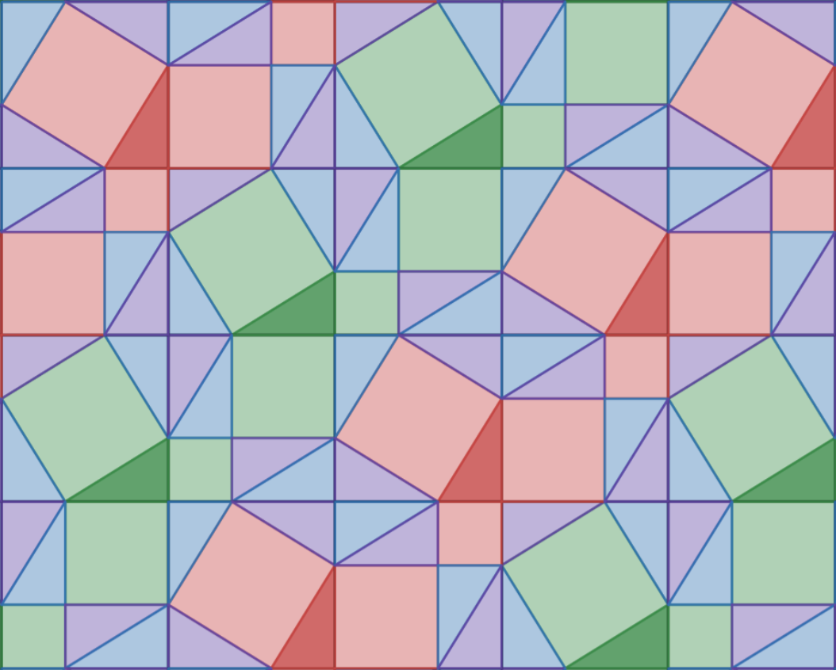
Pythagorean Tiling
This is a graphical demonstration of the Pythagorean Theorem. First look at the red or green squares on the three sides of the darker right-angle triangles. We want to show that the area of the (tilted) square on the hypotenuse equals the area of the two other squares.
Now look at any two of the adjacent larger squares that make up the tiles of a rectangular grid. One contains the hypotenuse square, plus four copies of the original right angle triangle. The other contains the two other squares, plus the same four copies of the right angle triangles. Therefore those two squares must have the same area as the hypotenuse square.
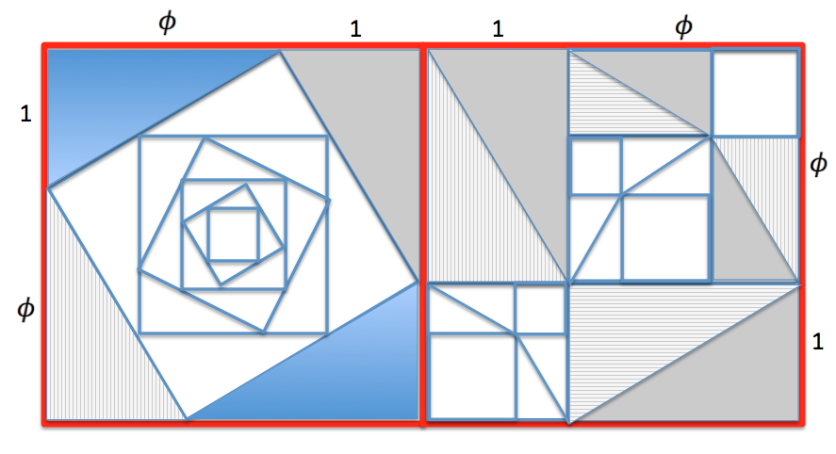
The Golden Pythagorean Fractal
To make this look nicer, we can make the ratio of the two sides of the right angle triangle equal to the golden ratio. Then we can reproduce the contents of the larger square inside the smaller squares to obtain a fractal effect.