This page explains how a very fast moving train can apparently fit into a tunnel that is shorter than the train. First, watch the first part of theYouTube video linked below. Then, relate the events in the video to the Minkowski space-time diagram that follows, or experience it in the Desmos calculator:
A train, travelling near the speed of light, passes through a short tunnel with gates on both ends. The stationary observer sees the train’s length as shortened, so it fits in the tunnel. Both gates close simultaneously when the train is entirely inside the tunnel, and then open again before it leaves.
In the moving train’s frame of reference, the train is longer than the tunnel. Both observers must see the train enter and leave the tunnel, and observe the same gate opening and closing events. The gates must not close while the train is over them. However, the train experiences these events occur in a different order.
The train cannot be treated as a single event because it exists across multiple locations in space. Therefore the motion of the front and back of the train is shown with two separate world lines. The time experienced by the train is defined by lines parallel to its space (x’) axis, shown here as dashed lines with sequence numbers.
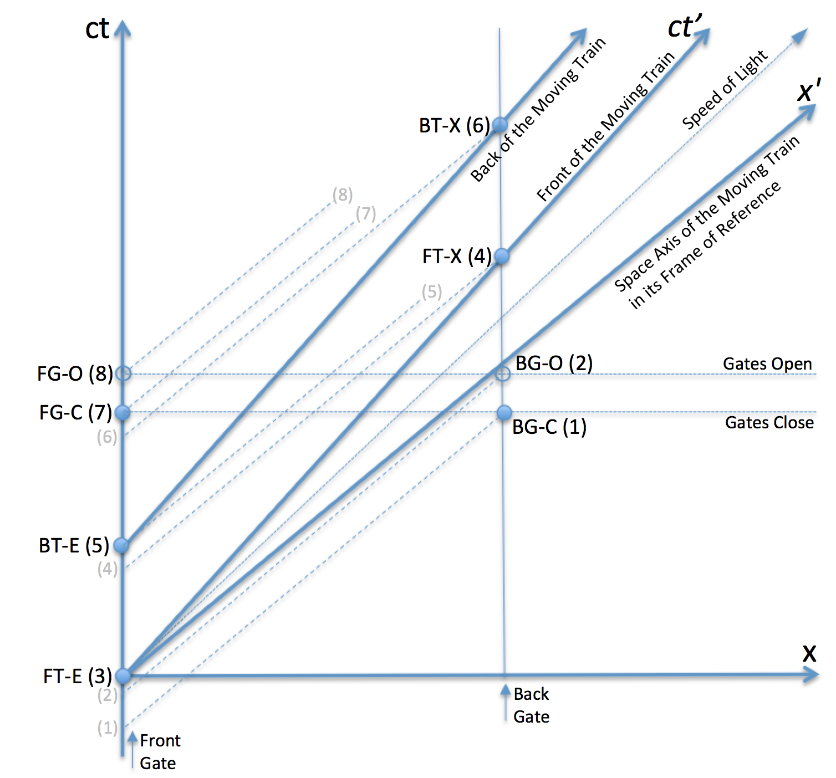
All the events (shown by dots with three-letter labels) take place in space at the front and back gates of the tunnel. The vertical world lines are the same in both frames of reference. The numbers refer to the moving train’s frame of reference.
In the stationary frame of reference, simultaneous events in time are horizontal lines parallel to the x-axis. The events happen in the following order:
FT-E The front of the train enters the tunnel.
BT-E The back of the train enters the tunnel.
FG-C, BG-C The front and back gates close, enclosing the train in the tunnel.
FG-O, BG-O The front and back gates open while the train is still in the tunnel.
FT-X The front of the train exits the tunnel through the open gate.
BT-X The back of the train exits the tunnel.
In the moving train’s frame of reference, simultaneous events in time are the dashed lines parallel to the x’-axis. All events are projected to the front gate (on the stationary time axis) and indicated with numbers in brackets. In principle they should be shown on the train’s time axis, but that would make the diagram difficult to draw. Both ways show the events in the same order.
From the train’s point of view, the events occur in the following order:
BG-C(1) The back gate closes before the train arrives.
BG-O(2) The back gate opens in time for the train to arrive.
FT-E(3) The front of the train enters the tunnel through the open gate.
FT-X(4) The front of the train exits the tunnel before the back enters.
BT-E(5) The back of the train now enters the tunnel.
BT-X(6) The back of the train exits the tunnel.
FG-C(7) The front gate finally closes, after the train has left.
FG-O(8) The front gate opens again.